Introduction
This quarter (FQ23), I am teaching our lower-div course on computer organization
and assembly language (ECS 50). The first couple of weeks are dedicated to how
various types of data are represented in the computer. For instance, we study
unsigned integers, signed integers, characters, and floating-point numbers.
In one of my slides about floating-point numbers, I briefly mention that the
exponent is stored as a “biased value” but every time in lecture, I struggle to
decide how much details I should provide. If I don’t give much detail, then
students can get confused as to why the exponent’s value is simply not stored
directly as a signed integer. On the other hand, if I start diving into the
reasons for storing the exponent as a biased value, I could probably spend a
whole lecture on it!
So I decided to explain the whole reasoning behind the exponent bias here
(spoiler: it has to do with comparisons between floating-point numbers). This
way I’ll be able to refer students to this article next time I teach this class!
Unsigned integers
Let’s start from the beginning with the representation of unsigned integers.
Unsigned integers are integers that can hold a null or positive value.
The bits composing an unsigned integers directly represent their magnitude, by
adding the corresponding powers of two. So, for example, when considering 8-bit
word 01101000 as an unsigned integer, it gets interpreted as
$0*2^7 + 1*2^6 + 1*2^5 + 0*2^4 + 1*2^3 + 0*2^2 + 0*2^1 + 0*2^0 = 64 + 32 + 8 = 104$
in decimal.
Comparison of unsigned integers
Comparing the magnitudes of two unsigned words is conceptually straightforward.
Starting from the most significant bit (MSB), the first integer that has a 1
that the other doesn’t is the greater number. Here is an example between two
8-bit words that contain unsigned integers:

In practice, hardware comparators are able to compare all the bits of two N-bit
words at the same time (say, words A and B), and output whether A < B, or
A > B, or A == B.
Here is an example of a 4-bit comparator:
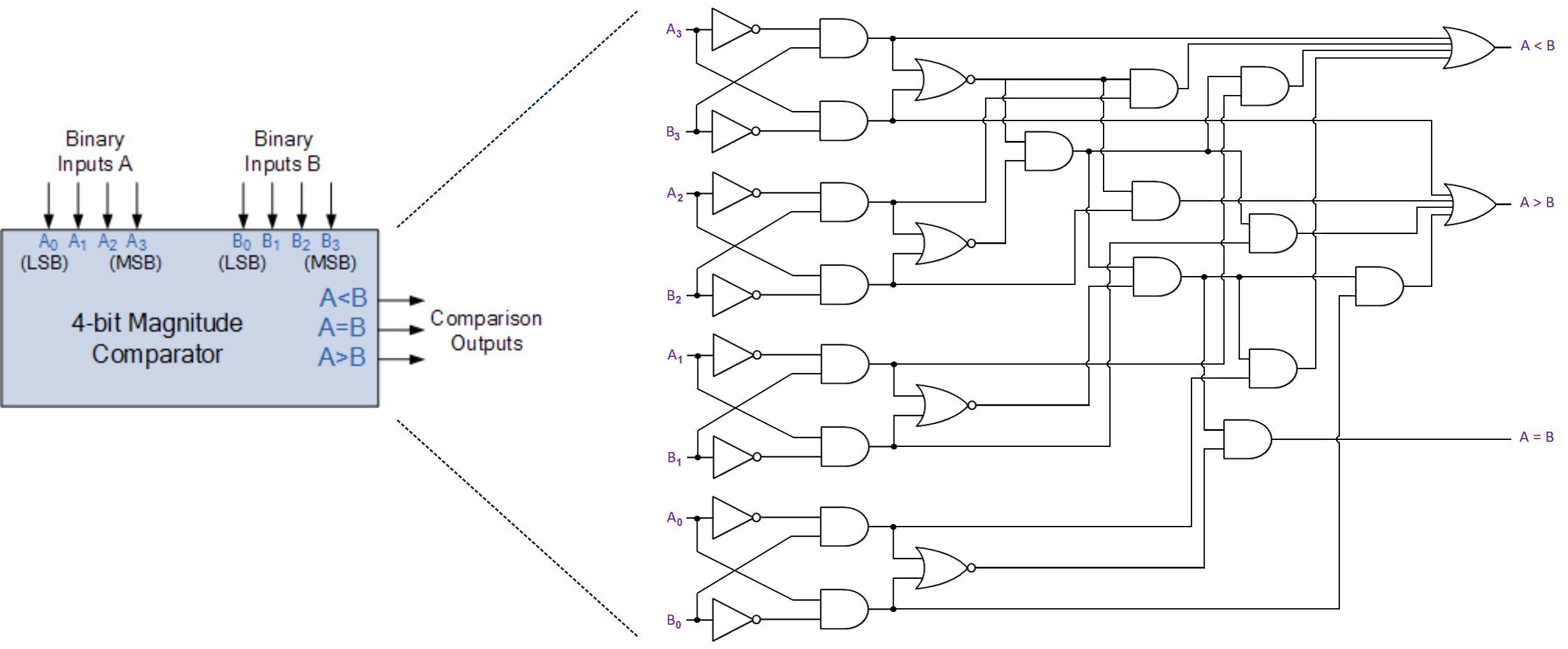
Signed integers
Signed integers are integers that can hold a negative, null, or positive value.
The most common approach to encode signed integers is called two’s complement.
In this approach, the word’s MSB acts as a sign bit. If a signed word has its
MSB set to 0, then it contains a positive value which can be decoded by simply
determining the magnitude represented by the remaining bits (just like the
unsigned interpretation). In that case, the sign bit itself carries no value
(i.e., it is not associated to a power of two), which makes sense since it’s
worth 0 anyway.

However, if the sign bit is 1, then it is meant to represent a base value of
$-2^{w-1}$ where $w$ is the word size. The remaining $w-1$ bits are then
interpreted as an unsigned integer, and represent a (positive) offset from the
negative base value set by the sign bit.

Comparison of signed integers
Comparing two signed words is slightly more involved than with unsigned
integers.
- If the two signed integers have opposite sign bits, then the integer with the
positive sign (i.e., sign bit of
0) is the greatest. We don’t even need to
compare any other bits.
- If the two signed integer have the same sign bit, then we have to compare
their magnitude (expressed by the $w-1$ remaining bits).
- For positive signed integers, it’s straightforward since the magnitude
directly encodes the value.
- For negative signed integers, it actually just works too, since the
integer with the bigger (positive) magnitude will be the one that is the
further away from the negative base value, which means the closest to 0,
which means the greater number! See example below.
- In either case, we can use the same type of comparator as for unsigned
integers, but only on the $w-1$ lower bits.
Here is an example of comparing two negative numbers:

Floating-point numbers
Floating point numbers are typically represented using the IEEE 754 standard, in
their binary normalized scientific notation: $\pm~M*2^E$.
Intro
For example, number $+1101.1001$, which represents $+ 2^3 + 2^2 + 2^0 + 2^{-1} +
2^{-4} = +13.5625$ in decimal, can be rewritten as $+1.1011001*2^3$ in its
binary normalized scientific notation. The sign is positive ($+$), $M$ is known
as the mantissa and only has one digit before the binary point ($1.1011001$),
and the exponent $E$ (worth $3$ here) is the power of two multiplying the
mantissa to adjust the binary point.
This is akin to representing rational decimal numbers using the normalized
scientific notation. For instance, number $-4,321.768$ can be expressed as
$-4.321,768 * 10^3$.
In single precision (i.e., float in C), a floating point number is encoded in
a 32-bit word. In this format, the sign is expressed by the top bit, the exp
field on 8 bits is meant to represent the exponent $E$, and the frac field
on 23 bits represents the fractional part of $M$.

If $E$ is negative, we can represent very tiny numbers, such as
$1.0*2^{-42}=0.000,000,000,000,227,373,675,443,232,1$. If $E$ is positive, we
can represent very large numbers, such as $1.0*2^{42}=4,398,046,511,104$. Since
exp is on 8 bits, it gives 256 possible combinations that we can use to
represent a contiguous range of negative and positive numbers centered around
$0$. For example, if we assumed some standard two’s complement method, it could
represent range $[-128,127]$ (it’s just an example though, because it is not
what exp represents).
Given a certain value $E$, all the combinations of frac give $2^{23}$
equispaced values in the range $[2^E,2^{E+1})$. If $E$ is incremented by one, it
opens a new interval of $2^{23}$ equispaced values, which has no overlap with
the previous interval.

In terms of comparison, we can then already observe a few things. First, if two
numbers have opposite signs, then the positive number is automatically the
greatest. Otherwise, we have to then consider the signed value of $E$. That is,
between two floating-point numbers, the one with the greatest $E$ value is the
greater number. Finally, if both numbers have the same sign and the same $E$,
then the number with the greatest $M$, that is the greatest frac field, is the
greater number.
$E$ is actually not directly stored in exp as a signed integer, as
hypothesised above. Instead, it is stored as a “biased value”. This means that
$E$, which is meant to belong to a contiguous range of 256 negative and positive
numbers centered around 0, is offset by a bias in order to be stored in exp as
a strictly positive value (i.e., an unsigned integer).
The bias for single-precision floating-point numbers (float) is set to $127$.
So for instance, if, for a given float, the exp field contains combination
00101010 (decoded as an unsigned integer as $42$), it would in fact represent
an exponent $E = 42 - 127 = -85$, which is negative. The float would be a rather
small number.
In this other direction, if we tried to represent a large floating point number
such as $1.frac * 2^{42}$ (we don’t care about the mantissa here), then $E$
would be equal to $42$, but it would be stored in field exp as $42 + 127 =
169$ after being offset by the bias.
Comparison of floating-point numbers
Why are we using this biased representation for $E$? Well, it has to do with
being able to compare floating-point numbers very quickly and efficiently!
Naive approach
Let’s start by considering the case where $E$ was stored in exp directly as a
signed integer, using the two’s complement method. In that case, the range of
$E$ would be $[-128, 127]$. If we had to compare two floats, it would be fairly
complex because we’d have to look at the sign bit, and then we’d have to apply
the comparison method for signed integers on the exp field:
- If the two floats have opposite sign bits, then the float with the
positive sign (i.e., sign bit of
0) is the greatest. We don’t even need to
compare any other bits.
- If the two floats have the same sign bit, then we have to compare
their
exp field as signed integers (same technique as explained above).
- If the two signed exponents have opposite sign bits, then the exponent
with the positive sign (i.e., sign bit of
0) is the greatest.
- If the two signed exponents have the same sign bit, then we have to compare
their magnitude (expressed by the $7$ remaining bits).
- For positive signed integers, it’s straightforward since the magnitude
directly encodes the value.
- For negative signed integers, it actually just works too, since the
integer with the bigger (positive) magnitude will be the one that is the
further away from the negative base value, which means the closest to 0,
which means the greater number!
- In either case, we can use the same type of comparator as for unsigned
integers, but only on the $7$ lower bits.
- If the two floats have the same exponent, then we have to compare their
frac
field as unsigned integers. Whichever float has the largest magnitude is the
greater number.
As you can see, we have to nest the signed comparison of the exponent, after
having considered the sign of the floats themselves. Doing this type of
comparison would require a specific, and complicated type of comparator.
Biased approach
Now, if we store the exponent of a floating-point number as a biased value, it
becomes an unsigned integer, which considerably simplifies the comparison of two
floats. In that case, the comparison becomes:
- If the two floats have opposite sign bits, then the float with the positive
sign is the greatest. We don’t even need to compare any other bits.
- If the two floats have the same sign bit, then we can compare all the
following bits as a magnitude.
- The number with the bigger exponent will appear to have a bigger
magnitude.
- If the two numbers have the same exponent, the fractional part of the
mantissa will become relevant and whichever has the bigger fractional part
will also appear to have a bigger magnitude.
- In either case, we can use the same type of comparator as for unsigned
integers, on all the bits after the sign bit.
Hopefully, you’ve noticed that we can use the same type of comparator as for
signed integers to compare floats, which makes things so much easier since we
already have them in any standard processor!
Conclusion
By storing the exponent of a floating-point number as a biased value, we enable
comparing floating-point numbers as if they were simple signed integers, that is
using the same type of comparator.
]]>
